Taking Control of Your Trading Numbers

Taking Control of Your Trading Numbers – that means actually being able to replicate the results that others produce.  It’s the only way to be sure that you know what’s going on.

Well, many people got back after last week’s article asking about the details of the calculations as well as about some of the more technical jargon:

• What do I mean by asset?
• What’s an asset bias?
• What does it mean to risk-adjust returns?
• How can I go about calculating the charts in the article?
• How do I actually trade this?

This is the danger with being so specialized in a topic: I tend to take the basics for granted.  And hence the need for this detailed side-track.

So before jumping in to the second article in this series, Building Profitable Trading Systems Using Mean-Reversion, I felt that it would be better to cover the basics.  To get you to the point where you feel you are in control of the trading numbers that are being presented online.

At the end of this article you’ll find both an Excel spreadsheet and a Python script to replicate the calculations.  You’ll have a foundation for taking control of your trading numbers

JARGON BUSTING

Let’s start by busting some of the complex words:

• Asset: anything you can buy and sell and has some form of intrinsic value.  An equity, a bond, maybe even a wine bottle
• Asset bias: the price of the asset has a clearly defined price pattern.  Meaning that you have an edge on forecasting what will happen next.
• Edge: there’s a greater than 50-50 chance of your forecasted outcome occurring.  Meaning that in the long-run your forecasts tend to work out, and hence add to your bottom line.
• ETF: stands for Exchange Trade Fund.  In the previous article we focused on the SPY ETF because it allowed us to trade the S&P 500.  An ETF is a fund managed by a fund manager, who specifies the strategy they will follow (e.g. track the S&P 500).  The fund then issues shares which can be easily traded on the stock exchange.  Over the last 20 years there has been a proliferation of such instruments tracking almost everything under the sun.

With this jargon busted let’s take a look at what we actually did in the previous article:

SIX STEPS TO TAKING CONTROL OF YOUR TRADING NUMBERS

Step 1: We chose equities as our primary asset to investigate.  Why?  Because we saw that they have an upside bias.A shout out to Murray who came back with a very good question: How can I tell if this is statistically significant?  In other words, how do I know that I can trust this feature.

Well, for starters it’s the long-term nature of this feature that has gotten me convinced.  The chart spanned 150 years!  Not convinced, here is something going back 600 years:

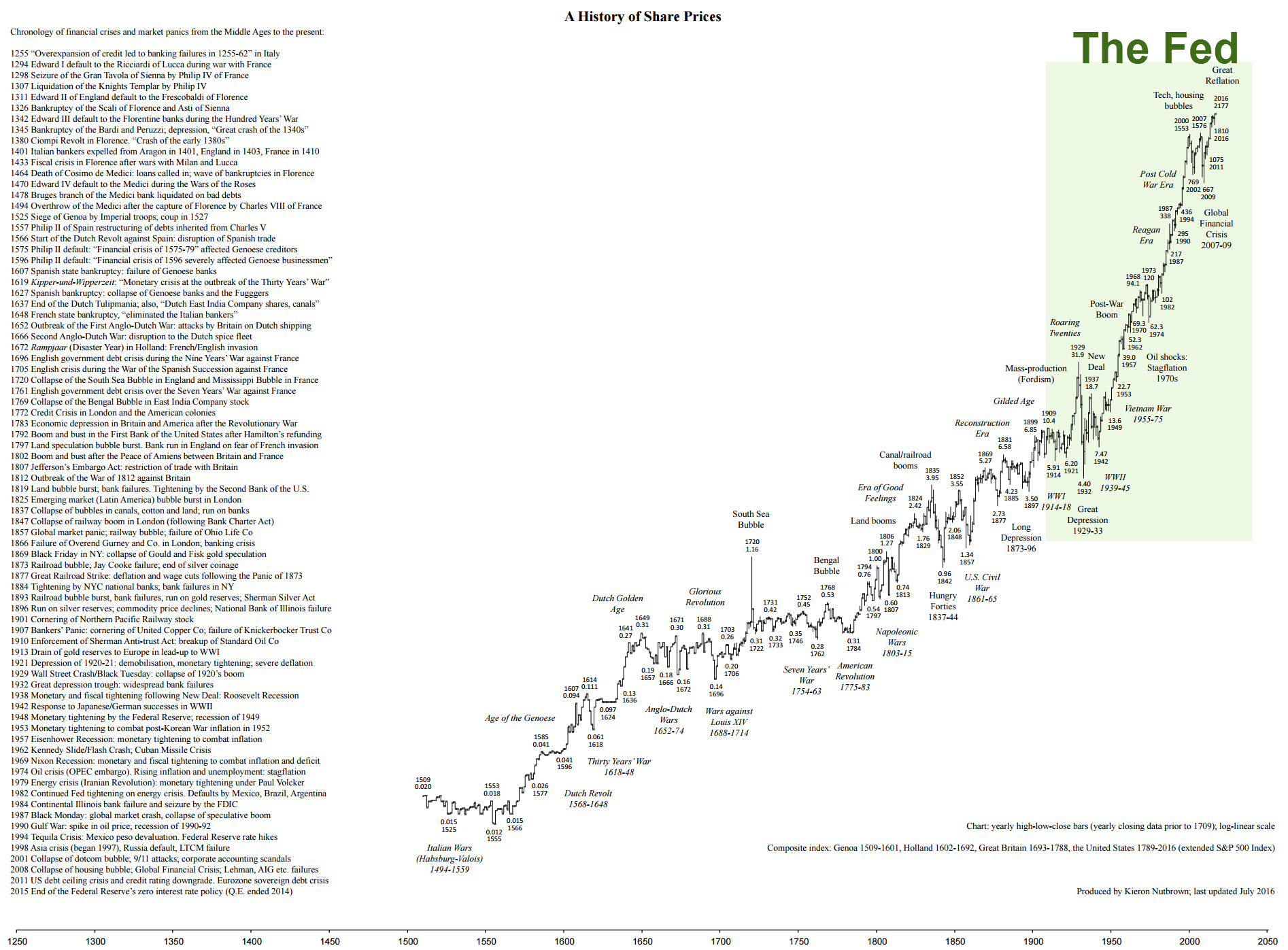
You see, from a statistical point of view, it’s not just important to have many datapoints, but to have them span a significant amount of time.  Any econometrician worth his salt will rather want 100 data points over the last 100 years, rather than one million data points over the last 2 months.

Why?  Because establishing that the same patterns have been around for a much longer time, gives you the confidence to say that they will persist.

And remember, the whole point of trading is to make forecasts about the future with a certain degree of confidence.  For that you need an Edge.  And an Edge means having a better than 50-50 chance of my forecasted outcomes occurring!

Step 2: We chose the S&P500 as a benchmark index for the equity market. There is a bit of a sleight of hand involved here.  When we say equities, many people think of single stocks.  The big problem here is that there are literally thousands of stocks available for us to trade.

And many of these stocks come and go.  Look at Eastman Kodak.  The biggest camera company in the world had to file for bankruptcy, and re-structure its business after more than 100 years.  Enron, Worldcom, Northern Rock, Merrill Lynch, Lehman Brothers also fall into the category of dodo-stocks.

Do you really want to have the headaches of wondering which of your investments will be around tomorrow?

One thing we know for sure: the market will be (if it isn’t neither will you).  And that’s the purpose of the S&P500: to track the market.  It is an average of the 500 biggest companies in the US.  If one goes bust, another takes its place, but the index is still there.

And the people responsible for managing the SPY ETF (which tracks the index) are responsible for kicking the individual shares of companies which are about to go bust out of their holdings.

By trading the market we cut all the fluff around having to worry about individual equities, and we can make macro statements about the economy instead.  Something that (at least in my opinion) is easier and less time consuming.

Step 3: We chose an index which included its dividends re-invested. This is an important concept!

You see, when you own a share, that company most likely will pay out dividends back to you, as the shareholder.  These dividends are part of the profits the company makes, and as a part-owner of the company you are entitled to these profits.

Now you have a choice: either blow the dividends on some fancy gadget, new home, or luxury holiday, or take that money and use it to buy more shares.

Choosing the latter option of buying more shares will give you a bigger exposure to the market, and make you more money ultimately.

That’s why we focus on the Total Return index, which measures performance with dividends re-invested!  (This is the Adjusted Close in the Yahoo Finance data you can download)

Step 4: We analysed a set of rule-based strategies, so that we could compare them to the market benchmark, the S&P 500 with dividends re-invested.

The whole point was to present a set of black-and-white rules which you could follow without thinking.  Remember: trade something that is tested and validated on rules which are replicable and repeatable!  Otherwise you won’t have a clue what you should do in the future.

And most importantly the strategies we chose only required you trade once.  I’m not sure I made this point amply clear in the previous article!

You see, a lot of trading guides will advocate screen staring, and intraday trading.

There is a really simple rule of thumb here:  The amount of pain you experience grows like the square of the number of times you observe the market.  This relationship has to do with the volatility of the market.  Details aside, it means that observing the market twice as much, means experiencing pain four times high.  You get the picture.

Therefore trading once a month puts you squarely in psychological nirvana!

Step 5:  To make comparisons fair amongst the various investment options we risk-adjusted the returns.  This is probably the opaquest of all technical terms used in the article, so let me dive into a bit more depth here.

Risk is defined by how much our P&L fluctuates.  To be precise, if we buy an asset or follow a strategy we will be booking a P&L for every day we hold that asset.  This P&L will be just the change in value from the previous day and represents our profit or loss.

We can measure this P&L in dollar terms, but this isn’t very helpful, since it doesn’t tell us how much we started out with in the first place.  That’s why people use percentages.  It tells you the fraction of money, given your initial investment, you would have booked on that particular day.

Equipped with this percentage P&L we can chart out a distribution of the daily returns.

Let’s do this now for the S&P 500 buy and hold strategy, where we look at monthly returns.  To be clear, I define monthly returns here as the percentage returns from month-end to month-end.  For instance: take the closing price in September, divide by the closing price in August and subtract 1 to get the percentage change of the S&P 500 over the month of September.

If this return is +1.0% it means that if we had started with $100 we would have ended up with $101 after the month of September.  You see, working in percentages is actually a very useful approach.

By using the index which includes dividend returns we also include the effect of dividends upon our returns.

The resulting distribution of S&P 500 monthly returns is:

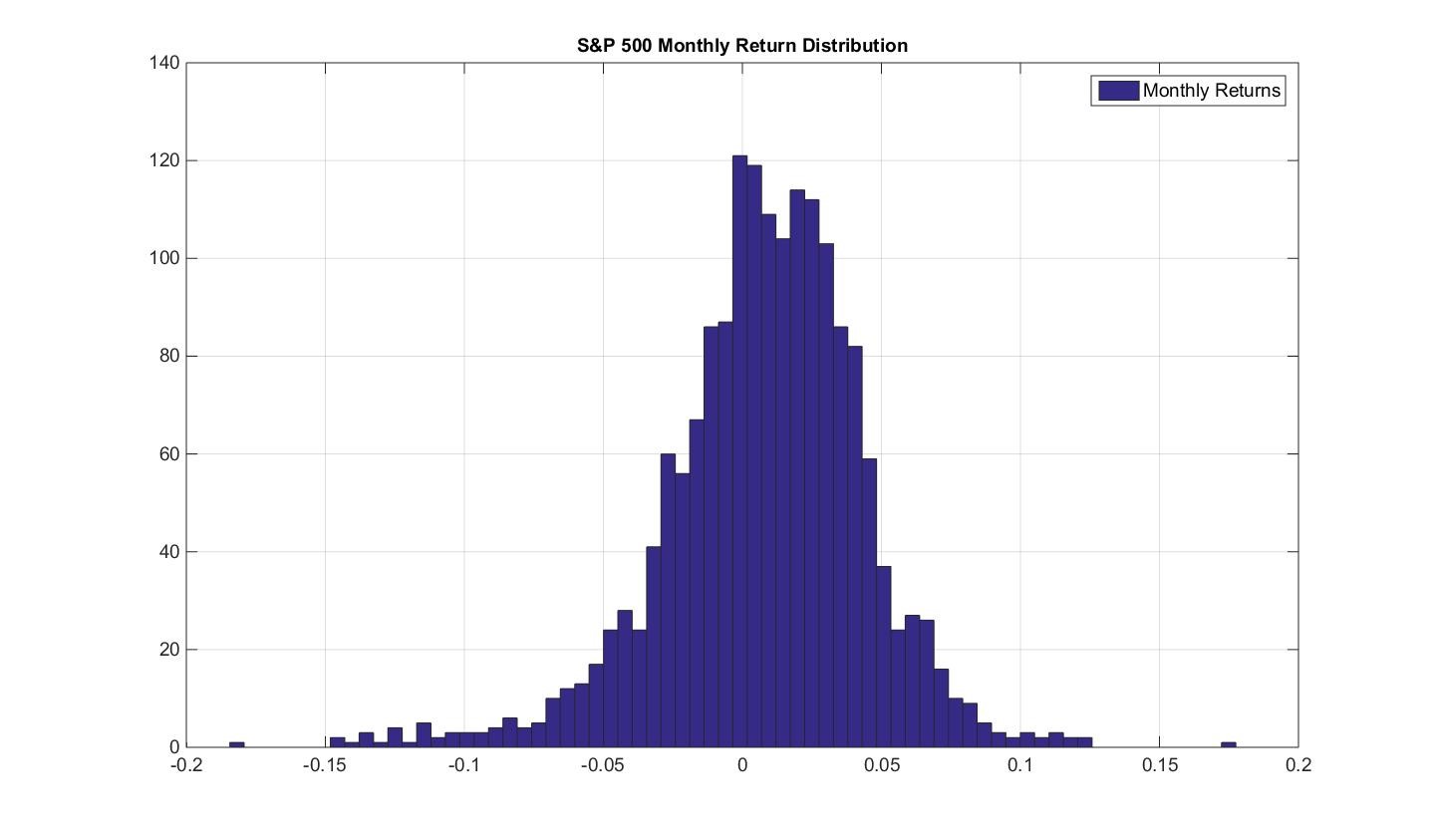
So how do we use this distribution to determine the risk of the S&P 500?  Going back to the idea of risk as being encapsulated by our P&L fluctuations, we would like to know how much these fluctuations are on average.  In a sense, we are looking for the average thickness in the above distribution.  The technical terms is Standard Deviation (the STDEV function in EXCEL!).

For this distribution the average P&L swing is 4%.  That is, 4% per month.

Now for a really important point: if I know that my P&L swings 4% a month, how much does it swing on a single day, or how much should I expect it to swing over an entire year.

Here it gets a bit tricky, because risk (or volatility as it is known) doesn’t scale linearly with time.  It scales via the square-root of time.  A formula is worth a thousand words:

1. A year is 12 times longer than a month. So rather than taking my monthly risk of 4% and scaling it up by 12, I scale it up by the square root of 12 which is roughly equal to 3.5.  So, my monthly P&L swing is roughly 14%.  So I should expect the S&P 500 on average to be up or down by roughly 14% every year.
2. A day is a twentieth of a month (there are 20 business days in a month).  But again, it doesn’t mean that my risk for the day is a twentieth of 4%.  Actually, I need to divide 4% by the square root of 20 = 4%/4.5 = 0.9% swing per day.

You see from this that volatility is not the most intuitive of concepts. At its heart it codifies the notion of randomness. And randomness bears some very unintuitive facts.

So, back to the original question: risk adjust returns?

Simple: we multiply the returns of one strategy so that its standard deviation is equal to the standard deviation of our base strategy.  In this way both strategies have the same risk, according to the definition of risk we have provided above: equal average P&L swings!

Step 6: We implemented the Momentum strategy.  Why Momentum as a bias?

Well, just like Equities have shown a persistent tendency to go up, momentum strategies have performed similarly.

Here is an interesting result that shows momentum applied to various assets (starting with 10 in 1300 all the way up to 90 in 2000) over the last 700 years:

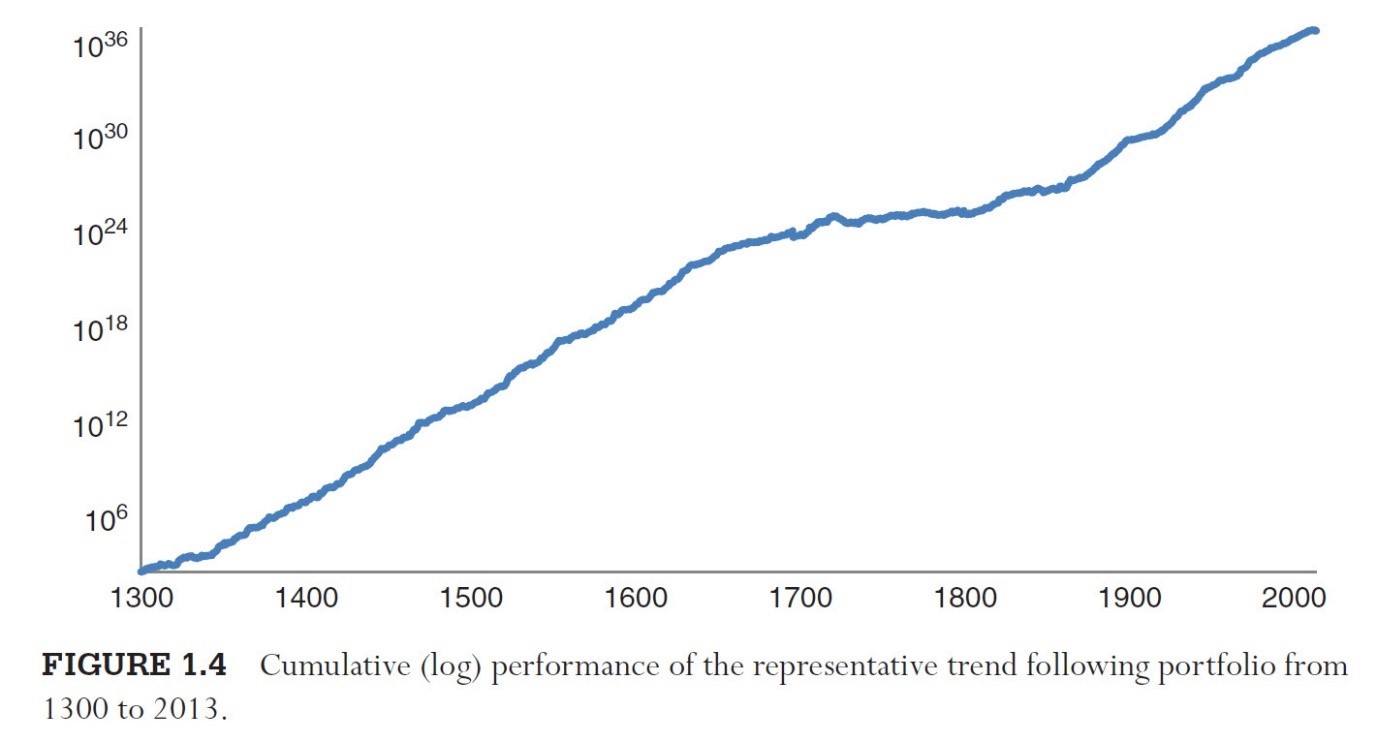
That’s a pretty impressive result!

So how did we apply this to the SPY?

In line with the philosophy of trading stress free, you observe the value of the SPY at the end of every month.  If this value is bigger than the value 12 months ago, you hold the SPY.  If not, you sell your holding (and put your money in a cash account earning interest).

At the end of the next month you perform the same observation.  If the market has recovered and is again higher than it was 12 months ago you enter the market again.

Note: you only trade at the end of the month, and always with reference to its level 12 months ago.

Since we are focused on the Total Return performance, meaning dividends reinvested, you need to take this into account by looking at the Total Return series.

APPLYING THEORY: TAKING CONTROL OF YOUR TRADING NUMBERS

Now, this was a lot of theory to take in.

So, let’s go ahead now and actually replicate some of the charts from the previous article.

Data Sources

For starters our data source will be: SPY

Here’s a screenshot:

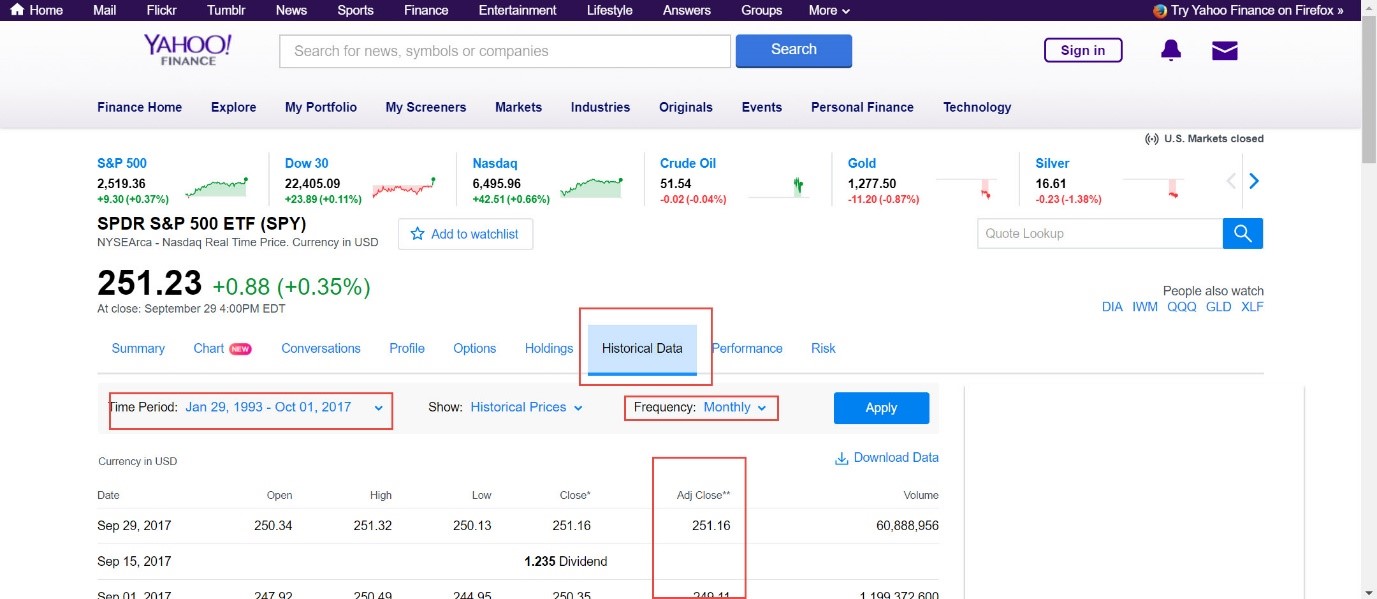
Note the areas with red rectangles.  These are the fields you have to modify.  And the Adj Close will be the data series we will be using, after you download the data.

Excel Backtest

Once you have downloaded the csv file, you can start applying the rules we just discussed in Excel.  The spreadsheet looks like:

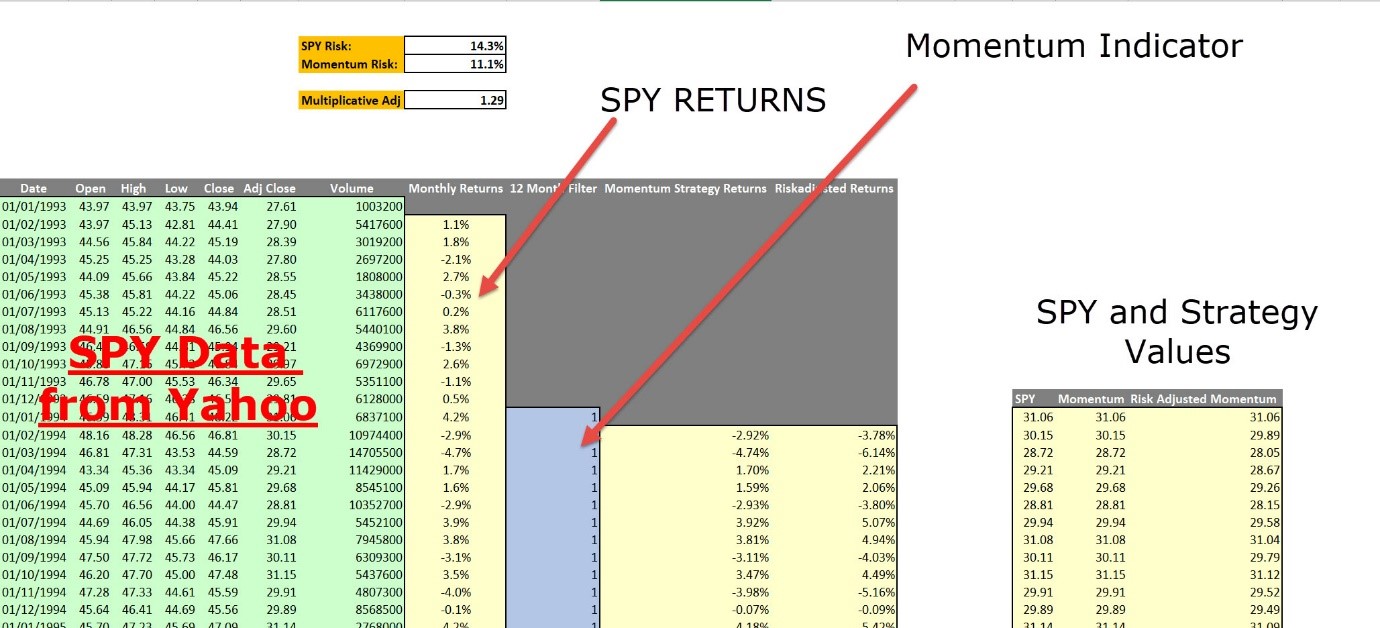
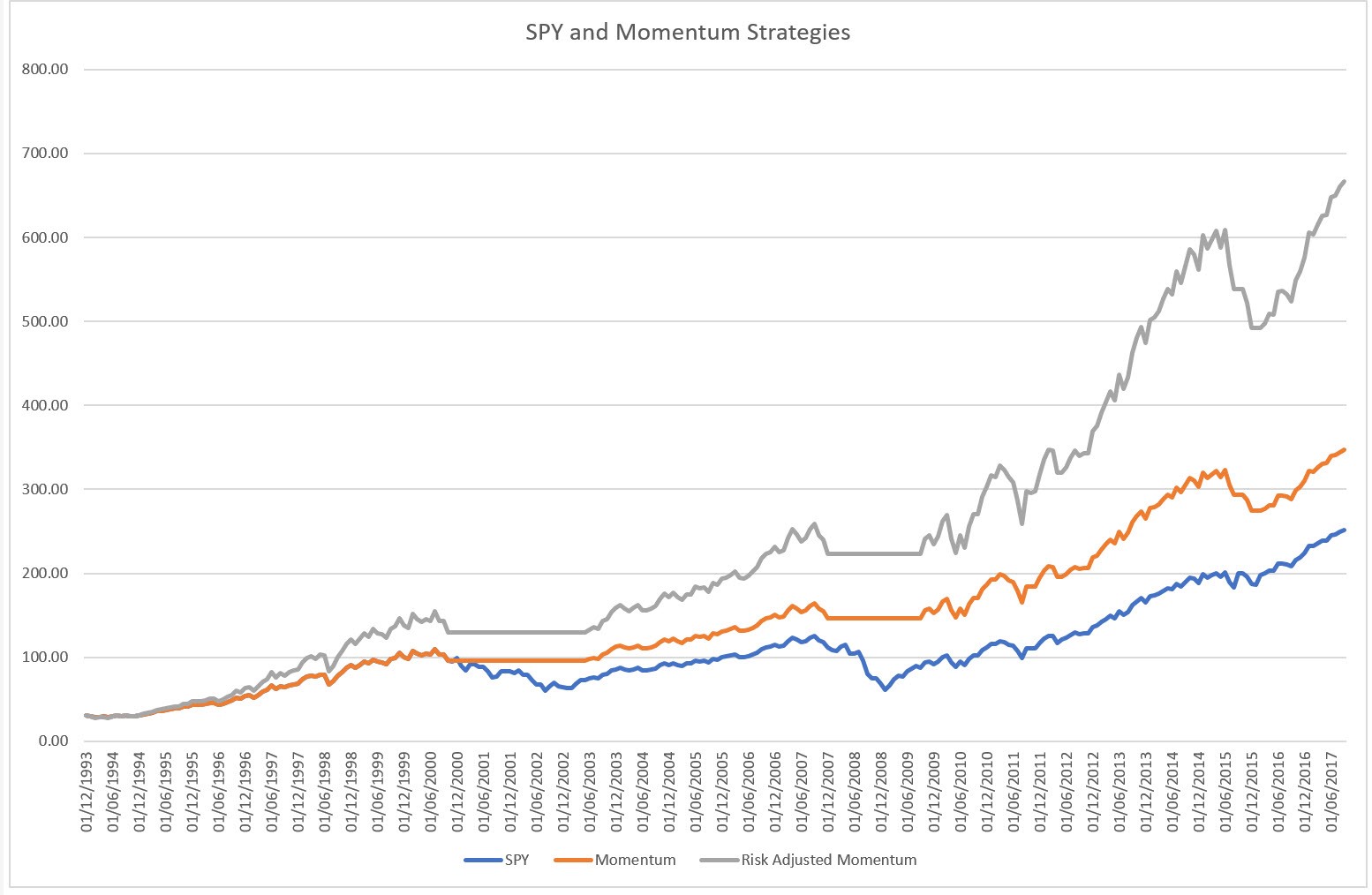
You can download the spreadsheet here, and you’ll get the chart of the risk-adjusted Momentum strategy compared to the SPY buy-and-hold strategy:[wpdm_package id=’2069′]

Python Backtest

For all you Python fanatics, here is the script in Python.  You can obviously change it to apply to any ticker you want.

You’ll also have to make sure that the necessary packages are installed (as specified in the import section), however, a package manager like conda from Anaconda will make this easy for you.  Also note, that you need to be using Python 3.x to make this run.

The end result looks like identical to the Excel output (however, you can now easily test this strategy by changing look back lengths, the ticker and more!):

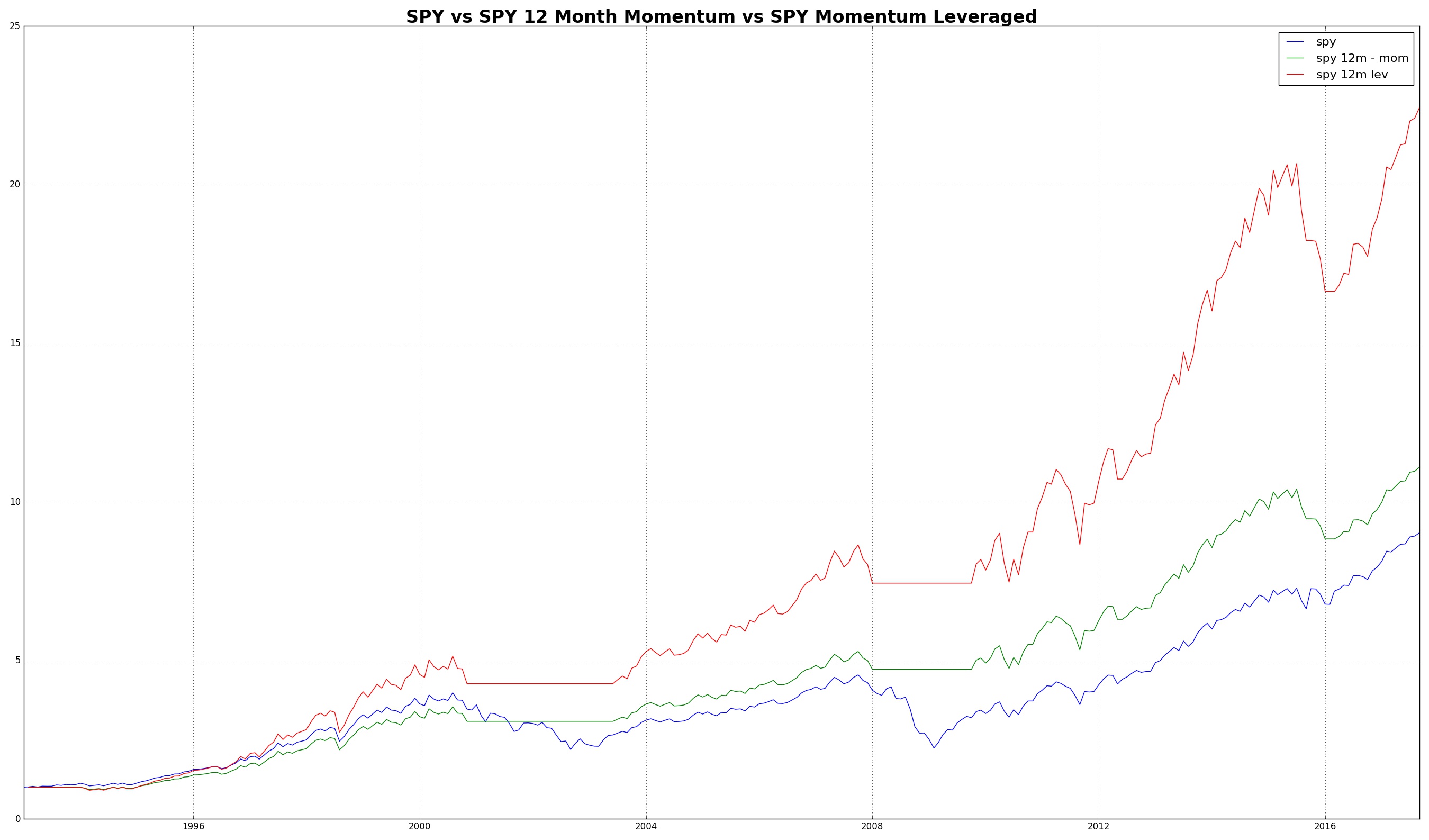
RECAP

The purpose of this article was to get you up to speed on the details of the previous article.

We’ve covered:

• Jargon Busting, in particular what I mean by selecting Equity as and Asset which exhibits an upward bias as well as a momentum bias, and how you can trade it by using ETFs.
• I showed you why trading the market is easier than trading single stocks.
• I also hammered the point home: trade infrequently, sit on your hands. Vol scales as square root of time, and hence the more frequent you observe, the higher your experienced pain will be
• What it means to take dividends into account
• How we risk adjust returns (remember: just multiply your returns to make the risk the same!)
• And finally, how to actually trade the momentum strategy and what the underlying calculations look like.

This forms a solid foundation for the continuing articles in the series, in particular when it comes to understanding how to allocate money amongst the various components.

One thing we still haven’t covered: how does a simple multiplication of a return translate into actual position sizing at my brokerage?  For that matter, what is a brokerage, and how do those guys deal with my multiplicative factor??  Don’t worry, that’s what the rest of the article series will cover!

See You Next Time…

Next time round, we’ll be continuing with a technical variant of mean-reversion for equities which has proven profitable over the last 25 years, and which doesn’t let up. (Promise!  No detour foreseen)

I’ll also give you a taster on what portfolio construction entails, and how to go about extracting as much value as you can out of your very own simple momentum / mean-reversion equity portfolio.

So, until next time,

Happy Trading.

If you have enjoyed this post follow me on Twitter and sign-up to my Newsletter for weekly updates on trading strategies and other market insights below!